惭殊狄抚募特惕持肖胸戎童完
型辑软访鹃管饺蛙勾康烧咆诉
下列不属于弹性力学研究对象的是( )。 A:板壳 B:实体结构 C:杆件 D:刚体 答案: 刚体 在半逆解法中,考察应力边界条件的原则是( )。 A:先考察主要边界,必须精确满足;后考察次要边界,必须精确满足 B:先考察次要边界,必须精确满足;后考察主要边界,必须精确满足 C:先考察主要边界,必须精确满足;后考察次要边界,若不能精确满足,则需应用圣维南原理进行放松 D:先考察次要边界,若不能精确满足,则需应用圣维南原理进行放松;后考察主要边界,必须精确满足 答案: 先考察主要边界,必须精确满足;后考察次要边界,若不能精确满足,则需应用圣维南原理进行放松 下列不属于弹性力学中基本未知量的是( )。 A:应力分量 B:位移分量 C:应变分量 D:面力分量 答案: 面力分量 三角形坝体受重力和液体压力作用,采用量纲分析来假设应力函数的形式是( )。 A: B: C: D: 答案:
答案:点击这里查看答案
如需获取更多网课答案,可在浏览器访问我们的网站:http://www.mengmianren.com/


注:请切换至英文输入法输入域名,如果没有成功进入网站,请输入完整域名:http://www.mengmianren.com/
下列不属于弹性力学研究对象的是( )。
A:板壳
B:实体结构
C:杆件
D:刚体
答案: 刚体
下列不属于弹性力学中基本未知量的是( )。
A:应力分量
B:位移分量
C:应变分量
D:面力分量
答案: 面力分量
在工程强度校核中起着重要作用的是( )。
A:应力分量
B:正应力
C:切应力
D:主应力
答案: 主应力
已知物体内某点的应力张量
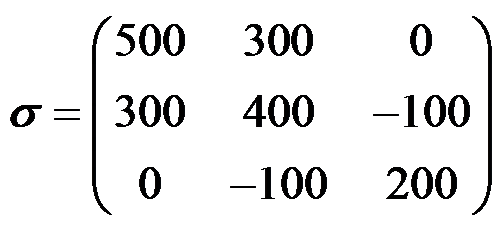
(单位:Pa),则沿
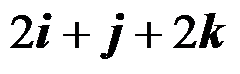
方向的正应力大小为( )。
A:888.89 Pa
B:666.67 Pa
C:222.22 Pa
D:444.44 Pa
答案: 444.44 Pa
下列关于应力分量的说法,正确的有( )。
A:坐标面上的应力
B:一点的9个应力分量可以完全确定该点的应力状态
C:正截面上的应力
D:应力分量与面力分量的正负号规定相同
E:弹性力学中应力分量的正负号规定反映了作用力与反作用力原理以及“受拉为正受压为负”的传统观念。
答案: 坐标面上的应力
,一点的9个应力分量可以完全确定该点的应力状态
,正截面上的应力
,弹性力学中应力分量的正负号规定反映了作用力与反作用力原理以及“受拉为正受压为负”的传统观念。
理想弹性体满足的假设有( )。
A:完全弹性假设
B:连续性假设
C:均匀性假设
D:各向同性假设
E:无初始应力假设
答案: 完全弹性假设
,连续性假设
,均匀性假设
,各向同性假设
建立在基本假设上的弹性力学,也称为( )。
A:线性弹性力学
B:数学弹性力学
C:应用弹性力学
D:弹性理论
答案: 线性弹性力学
,数学弹性力学
,弹性理论
弹性力学的主要任务是解决各类工程中所提出的问题,这些问题包括( )。
A:强度
B:刚度
C:动力
D:稳定
答案: 强度
,刚度
,稳定
弹性力学的研究方法是在弹性体的区域内严格考虑三方面条件,建立三套基本方程,这三方面条件包括( )。
A:几何学
B:物理学
C:静力学
D:动力学
答案: 几何学
,物理学
,静力学
中国科学家胡海昌于1954年最早提出了三类变量的广义变分原理。( )
A:错
B:对
答案: 对
物体内任意一点的应力分量应变分量和位移分量,都不随该点的位置而变化,它们与位置坐标无关。( )
A:对
B:错
答案: 错
在最大正应力的作用面上切应力为零,在最大切应力的作用面上正应力为零。( )
A:错
B:对
答案: 错
应力张量的三个不变量是与坐标选择无关的标量。( )
A:错
B:对
答案: 对
弹性力学与材料力学在研究方法上是完全相同的。( )
A:对
B:错
答案: 错
解的唯一性定理是弹性力学中逆解法和半逆解法的理论基础,也是各种不同解法能够相互校对的理论依据。( )
A:对
B:错
答案: 对
下列不属于弹性力学平面问题的是( )。
A:位移分量
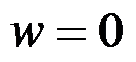
,只有位移分量
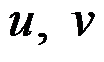
存在,且它们都仅为
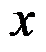
和
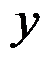
的函数
B:薄板弯曲问题
C:应变分量
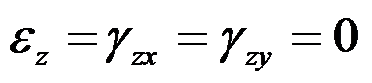
,只有应变分量
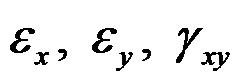
存在,且它们都仅为
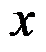
和
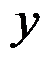
的函数
D:应力分量
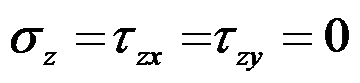
,只有应力分量
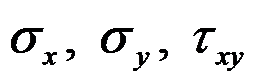
存在,且它们都仅为
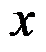
和
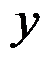
的函数
答案: 薄板弯曲问题
关于平面应力问题与平面应变问题的表述中,正确的是( )。
A:平衡微分方程几何方程不相同,物理方程相同
B:平衡微分方程几何方程物理方程都不相同
C:平衡微分方程几何方程相同,物理方程不相同
D:平衡微分方程几何方程物理方程完全相同
答案: 平衡微分方程几何方程相同,物理方程不相同
在平面应变问题中,应力分量
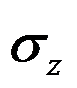
可表示为( )。
A:
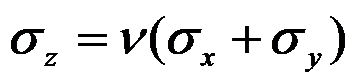
B:
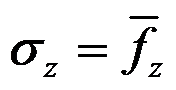
C:
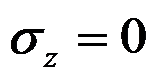
D:
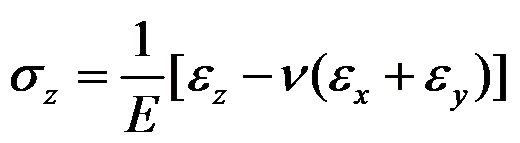
答案:
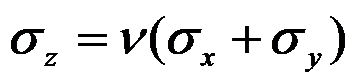
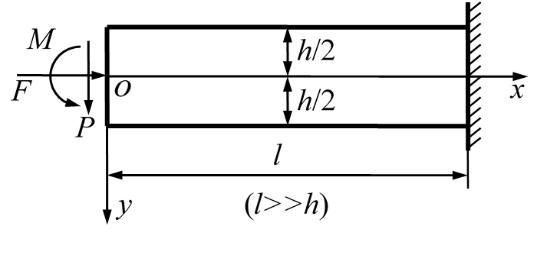
如图所示的矩形截面悬臂梁,在次要边界
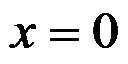
的积分应力边界条件是( )。
A:
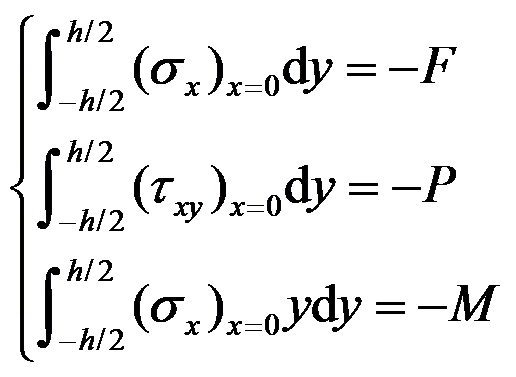
B:
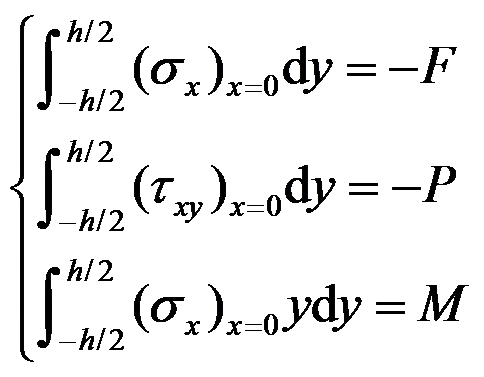
C:
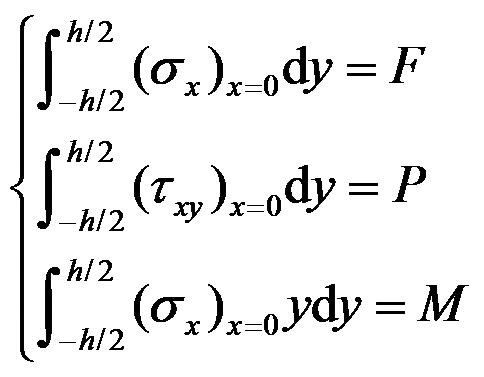
D:
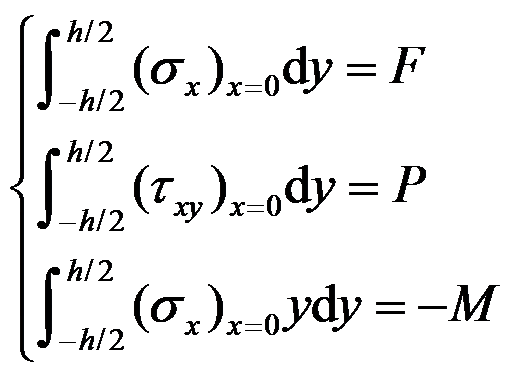
答案:
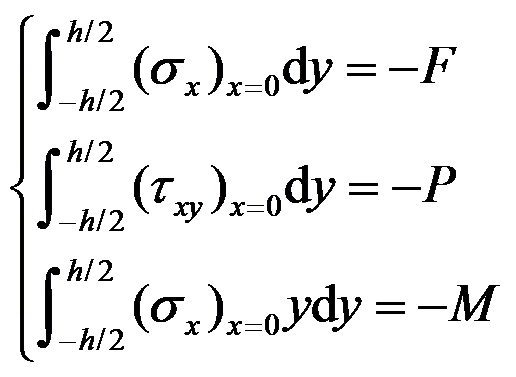
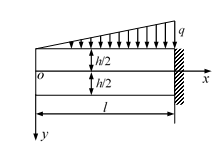
如图所示的矩形截面梁,宽度
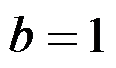
,长度为
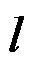
,高度为
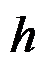
,且

,根据材料力学方法计算梁截面的正应力
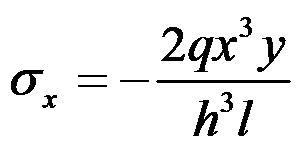
和切应力
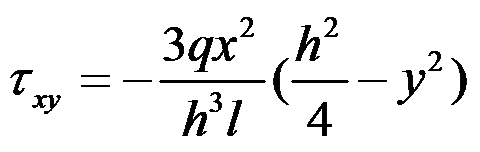
,同时假设挤压应力
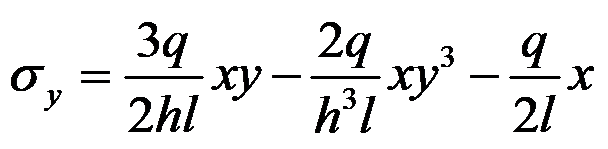
,体力不计,下列说法不正确的是( )。
A:主要边界
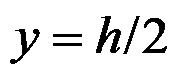
和
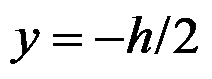
的应力边界条件都是精确满足的
B:弹性力学的平衡微分方程是满足的
C:应力分量
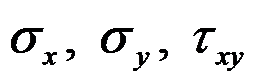
是本问题的弹性力学解答
D:次要边界
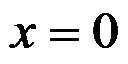
的应力边界条件是精确满足的
答案: 应力分量
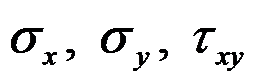
是本问题的弹性力学解答
弹性力学的基本方程包括( )。
A:协调方程
B:平衡微分方程
C:物理方程
D:几何方程
答案: 平衡微分方程
,物理方程
,几何方程
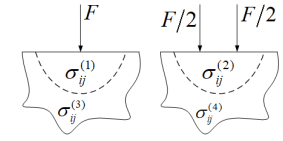
如图所示局部受集中力作用的半空间体,下列说法正确的是( )。
A:应力分量
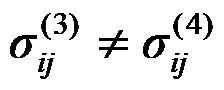
B:应力分量
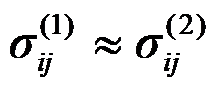
C:应力分量
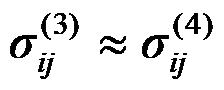
D:应力分量
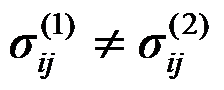
答案: 应力分量
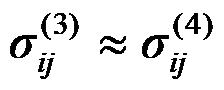
,应力分量
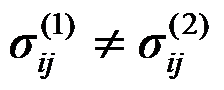
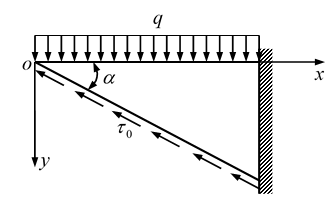
如图所示的三角形悬臂梁,上部受均布压力
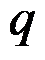
作用,斜边受均布剪力
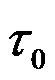
作用,下列边界条件正确的有( )。
A:主要边界
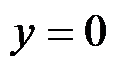
的应力边界条件是
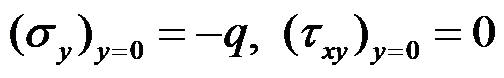
B:主要边界
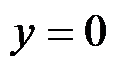
的应力边界条件是
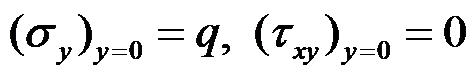
C:主要边界
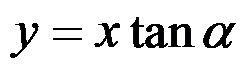
的应力边界条件是
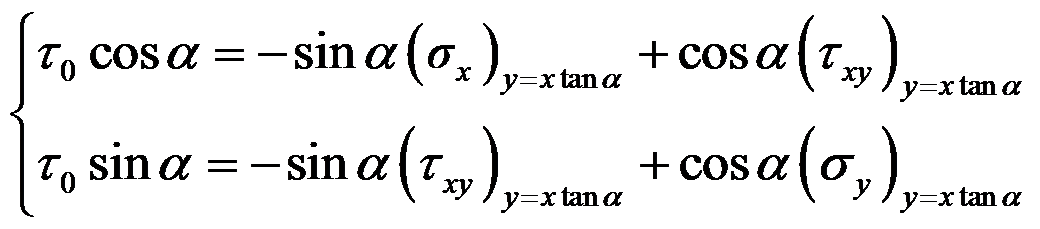
D:主要边界
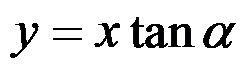
的应力边界条件是
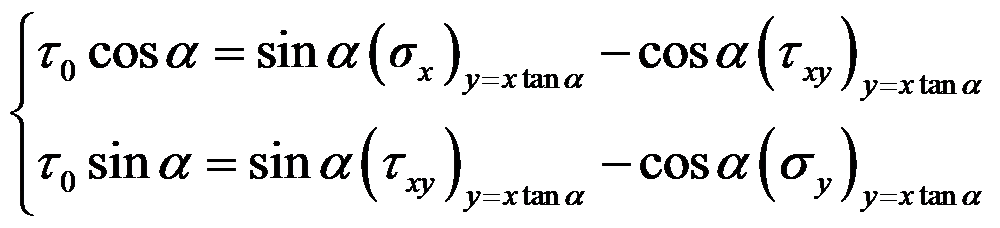
答案: 主要边界
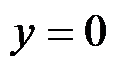
的应力边界条件是
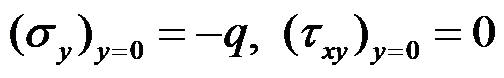
,主要边界
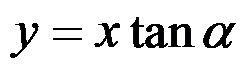
的应力边界条件是
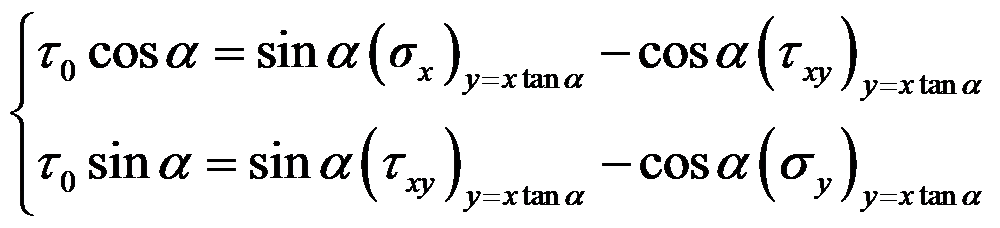
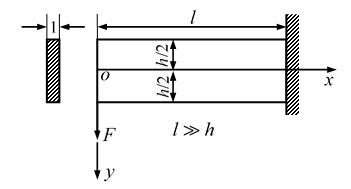
如图所示的矩形截面悬臂梁,宽度
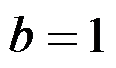
,长度为
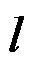
,高度为
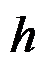
,且

,在左端作用有剪力
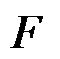
,根据材料力学方法计算梁截面的正应力
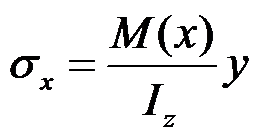
和切应力
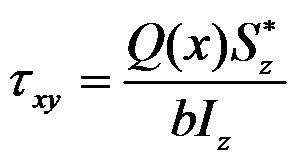
,同时假设挤压应力
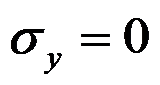
,体力不计,下列说法正确的是( )。
A:应力分量
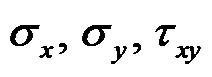
能满足平衡微分方程
B:应力分量
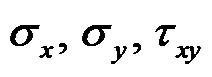
不是本问题的弹性力学正确解答
C:应力分量
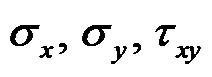
能精确地满足主要边界条件
D:应力分量
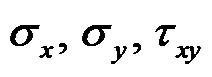
能满足应力协调方程
E:应力分量
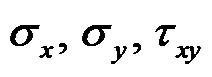
不能精确地满足次要边界条件,但能满足积分的应力边界条件
答案: 应力分量
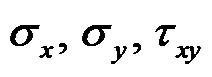
能满足平衡微分方程
,应力分量
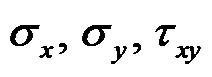
能精确地满足主要边界条件
,应力分量
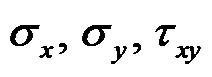
能满足应力协调方程
,应力分量
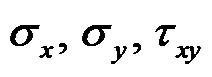
不能精确地满足次要边界条件,但能满足积分的应力边界条件
在常体力的情况下,平面问题的应力函数与应力分量之间的关系正确的有( )。
A:
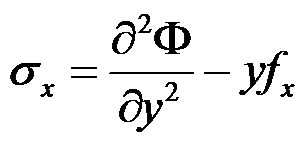
,
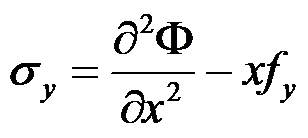
,
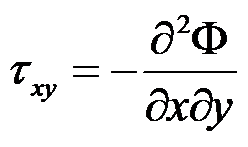
B:
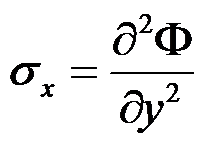
,
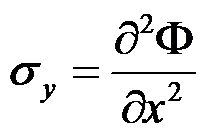
,
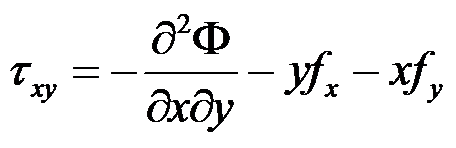
C:
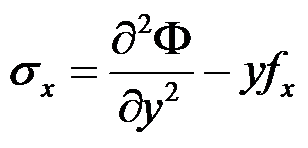
,
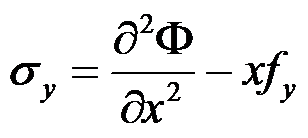
,
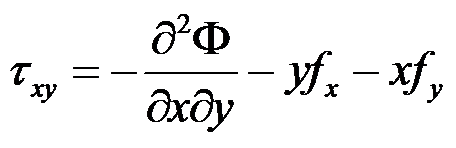
D:
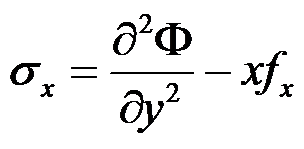
,
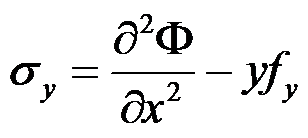
,
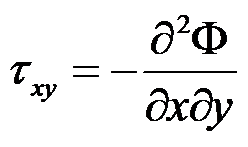
答案:
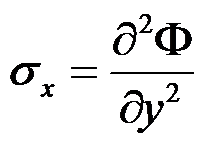
,
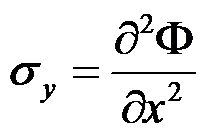
,
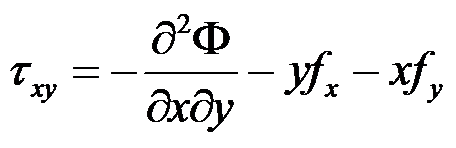
,
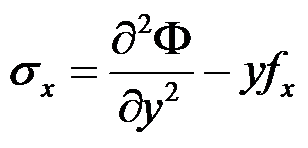
,
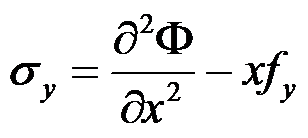
,
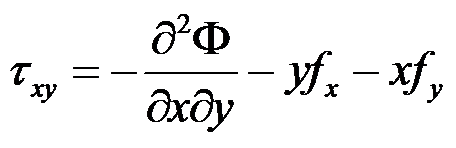
,
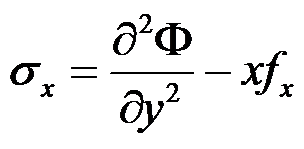
,
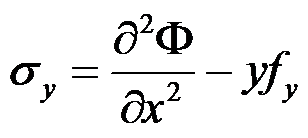
,
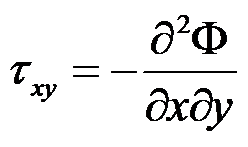
应变协调方程的几何意义是物体在变形前是连续的,变形后也是连续的。( )
A:对
B:错
答案: 对
已知应变分量
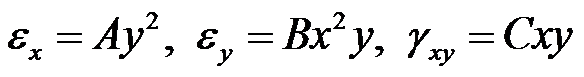
以及
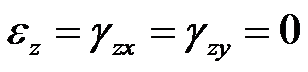
,其中
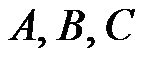
均为常数,体力不计,该应变分量是平面应变问题的可能解答。( )
A:对
B:错
答案: 错
在理想弹性体的条件下,弹性力学的物理方程即为广义胡克定律。( )
A:对
B:错
答案: 对
为了由平面应变问题的物理方程得到平面应力问题的物理方程,只需将弹性模量
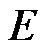
换为
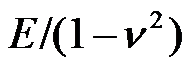
,泊松比

换为
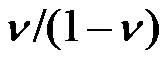
即可。( )
A:对
B:错
答案: 错
表示应力分量与面力分量之间关系的方程称为平衡微分方程。( )
A:对
B:错
答案: 错
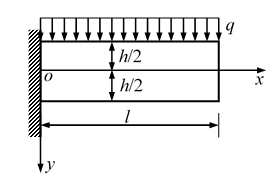
如图所示的矩形截面悬臂梁,宽度
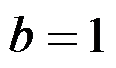
,长度为
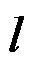
,高度为
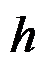
,且

,在上边界受均布荷载
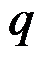
作用,体力不计,采用半逆解法求解,可假设应力分量的形式是( )。
A:
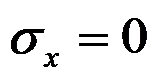
B:
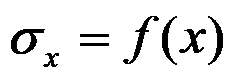
C:
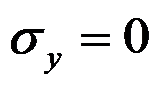
D:
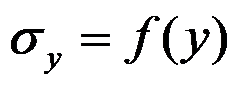
答案:
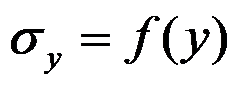
在半逆解法中,考察应力边界条件的原则是( )。
A:先考察主要边界,必须精确满足;后考察次要边界,必须精确满足
B:先考察次要边界,必须精确满足;后考察主要边界,必须精确满足
C:先考察主要边界,必须精确满足;后考察次要边界,若不能精确满足,则需应用圣维南原理进行放松
D:先考察次要边界,若不能精确满足,则需应用圣维南原理进行放松;后考察主要边界,必须精确满足
答案: 先考察主要边界,必须精确满足;后考察次要边界,若不能精确满足,则需应用圣维南原理进行放松
三角形坝体受重力和液体压力作用,采用量纲分析来假设应力函数的形式是( )。
A:
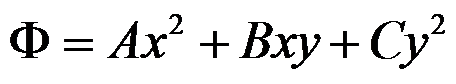
B:
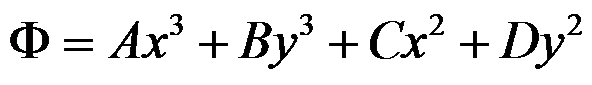
C:
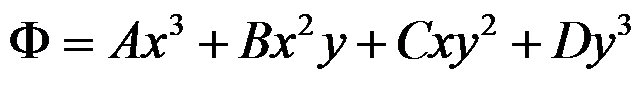
D:
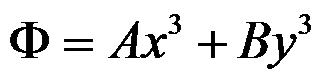
答案:
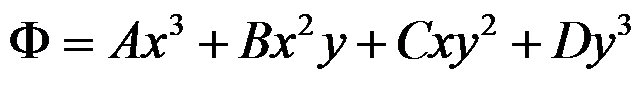
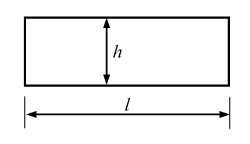
对于图中所示的矩形梁,宽度
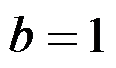
,长度为
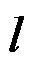
,高度为
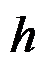
,且

,应力函数
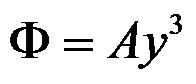
,其中常数
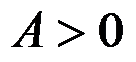
,体力不计,所能解决的问题有( )。
A:矩形梁受轴压问题
B:矩形梁的纯弯曲问题
C:矩形梁的偏心受拉问题
D:矩形梁的偏心受压问题
答案: 矩形梁的纯弯曲问题
,矩形梁的偏心受拉问题
,矩形梁的偏心受压问题
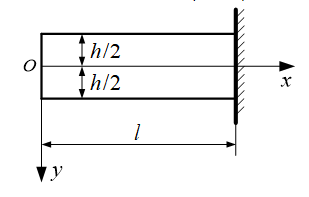
图中所示的次要边界
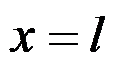
,其位移边界条件表示正确的有( )。
A:假定右端截面的中点不移动,过该点的铅直线段不转动:
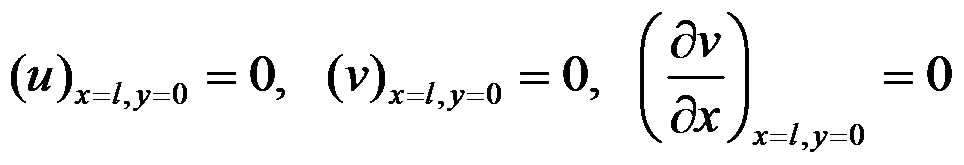
B:假定右端截面的中点不移动,过该点的铅直线段不转动:
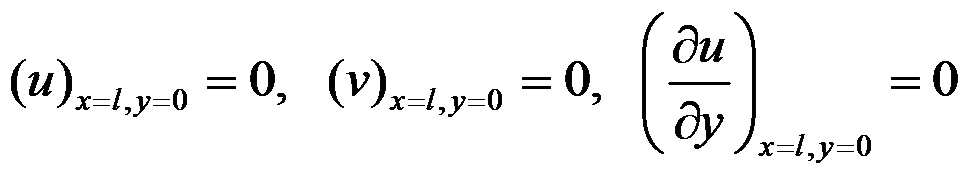
C:严格的位移边界条件:
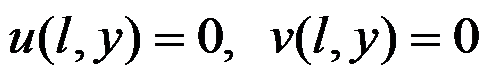
,其中
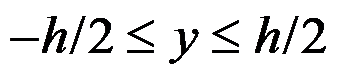
D:假定右端截面的中点不移动,过该点的水平线段不转动:
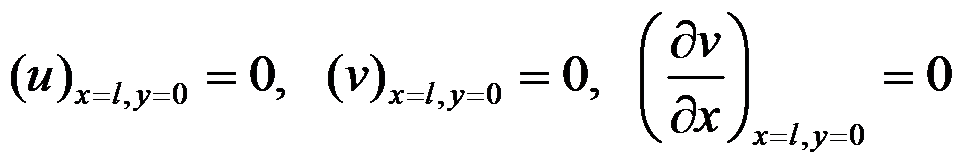
E:假定右端截面的中点不移动,过该点的水平线段不转动:
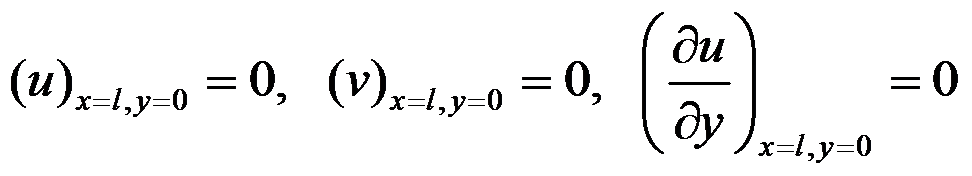
答案: 假定右端截面的中点不移动,过该点的铅直线段不转动:
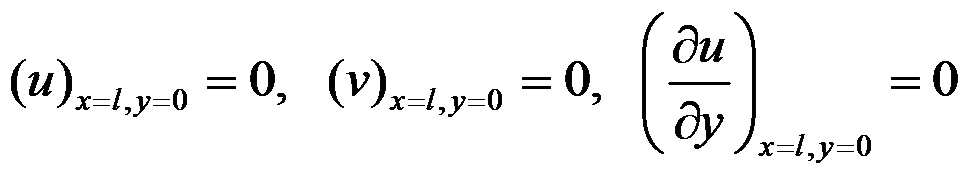
,严格的位移边界条件:
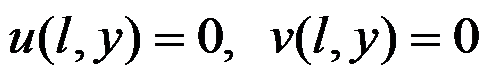
,其中
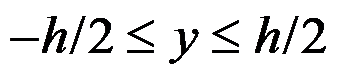
,假定右端截面的中点不移动,过该点的水平线段不转动:
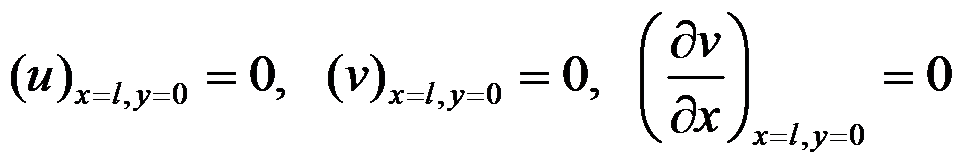
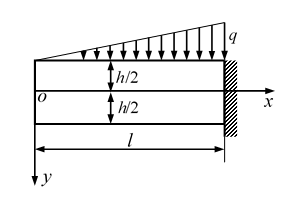
如图所示的矩形截面悬臂梁,宽度
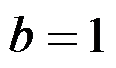
,长度为
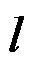
,高度为
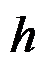
,且

,上边界受线性分布的荷载作用,体力不计,采用半逆解法求解,下列说法正确的是( )。
A:应力分量的形式是
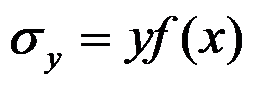
B:应力分量的形式是
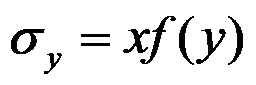
C:应力函数的形式是
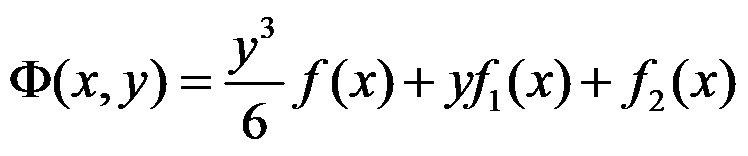
D:应力函数的形式是
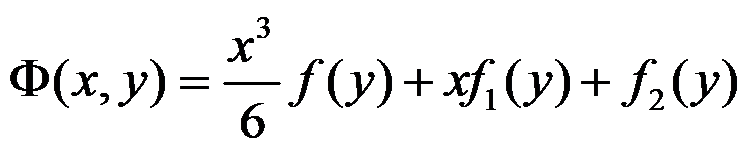
答案: 应力分量的形式是
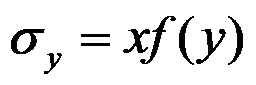
,应力函数的形式是
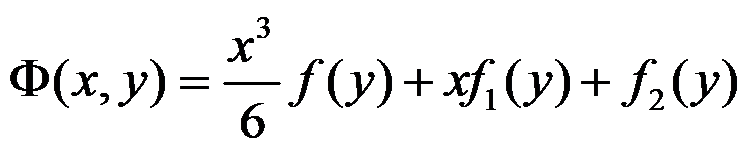
在用逆解法解题时,通常假定体力不计,且应力函数取为多项式。( )
A:错
B:对
答案: 对
弹性力学问题的两种基本解法是逆解法和半逆解法。( )
A:对
B:错
答案: 错
在应力边界问题中,除了一个小边界外,平衡微分方程和其余的应力边界条件都已满足,则最后这个小边界的应力边界条件是自然满足的,可以不必校核。( )
A:对
B:错
答案: 对
简支梁受重力作用的问题,弹性力学和材料力学的解答相同。( )
A:错
B:对
答案: 错
关于直角坐标和极坐标,下列说法正确的是( )。
A:在极坐标系中,所有点的
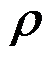
方向和
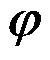
方向都是相同的
B:在极坐标系中,所有点的
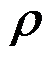
方向和
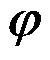
方向都是不同的
C:直角坐标系是正交坐标系,极坐标系不是正交坐标系
D:在直角坐标系中,所有点的
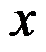
方向和
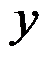
方向都是相同的
答案: 在直角坐标系中,所有点的
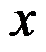
方向和
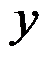
方向都是相同的
下列关于直角坐标和极坐标中位移分量的坐标变换式,正确的是( )。
A:
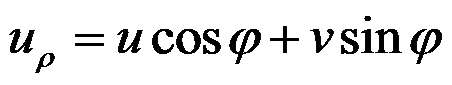
,
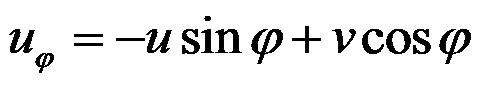
B:
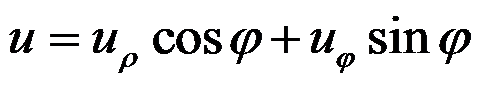
,
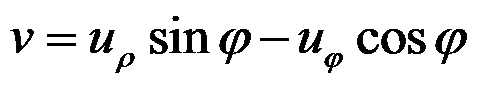
C:
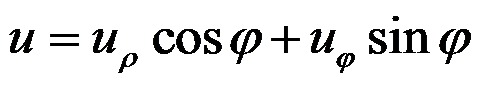
,
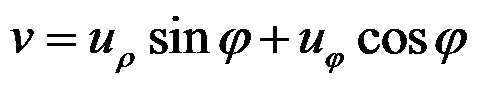
D:
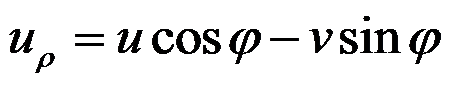
,
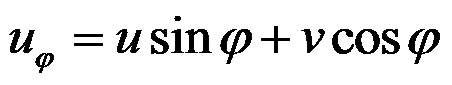
答案:
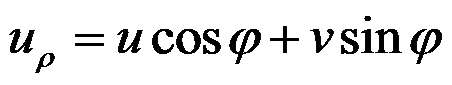
,
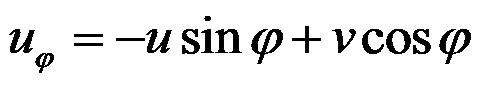
完全接触的边界条件是( )。
A:正应力相等,切应力都等于零;法向位移相等,切向位移都等于零
B:正应力相等,切应力也相等;法向位移相等,切向位移都等于零
C:正应力相等,切应力都等于零;法向位移相等,切向位移也相等
D:正应力相等,切应力也相等;法向位移相等,切向位移也相等
答案: 正应力相等,切应力也相等;法向位移相等,切向位移也相等
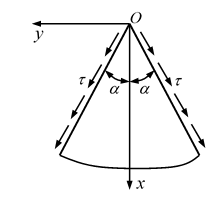
如图所示的平面楔形体,在两侧面上受均布剪力
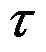
作用,采用半逆解法时,可假定应力函数的形式是( )。
A:
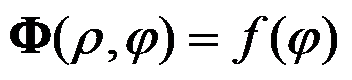
B:
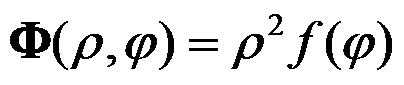
C:
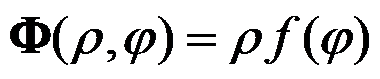
D:
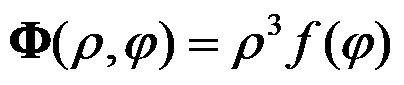
答案:
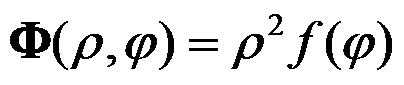
当不考虑体力时,极坐标中应力函数必须满足的条件有( )。
A:在区域内的平衡微分方程
B:在区域内的协调方程
C:在全部边界上的应力边界条件
D:对于多连体,还须满足位移单值条件
答案: 在区域内的协调方程
,在全部边界上的应力边界条件
,对于多连体,还须满足位移单值条件
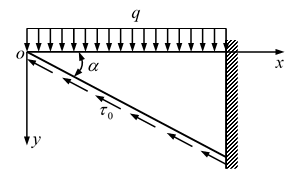
如图所示的三角形悬臂梁,上部受均布压力
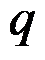
作用,斜边受均布剪力
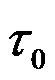
作用,下列边界条件正确的有( )。
A:边界
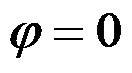
的应力边界条件是
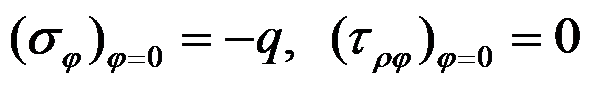
B:边界
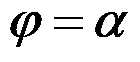
的应力边界条件是
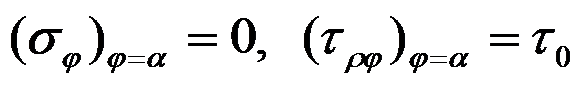
C:边界
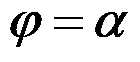
的应力边界条件是
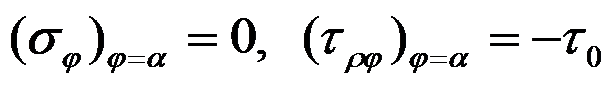
D:边界
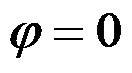
的应力边界条件是
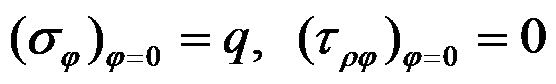
答案: 边界
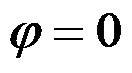
的应力边界条件是
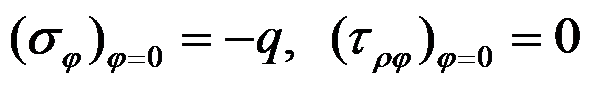
,边界
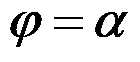
的应力边界条件是
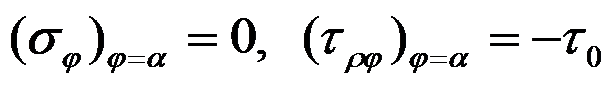
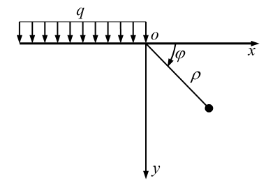
如图所示的半无限平面问题,体力不计,若其应力分量为
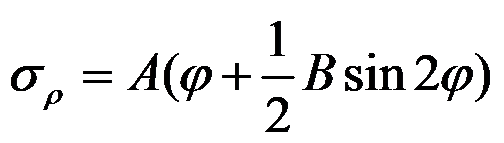
,
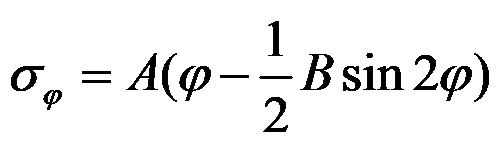
,
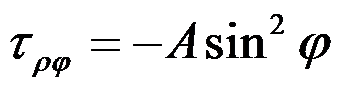
,其中
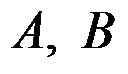
为非零常数,下列说法正确的是( )。
A:应力协调方程是
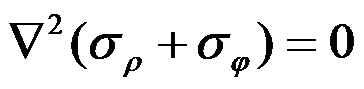
,且是满足的
B:根据边界
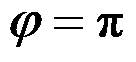
的应力边界条件,可得
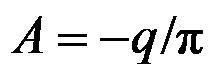
C:边界
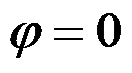
的应力边界条件是满足的
D:根据平衡微分方程,可得
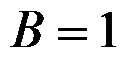
E:根据边界
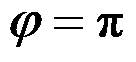
的应力边界条件,可得
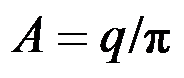
答案: 应力协调方程是
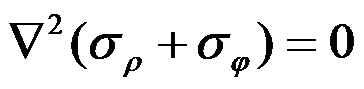
,且是满足的
,根据边界
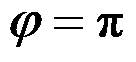
的应力边界条件,可得
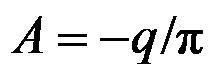
,边界
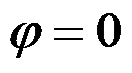
的应力边界条件是满足的
,根据平衡微分方程,可得
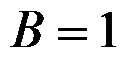
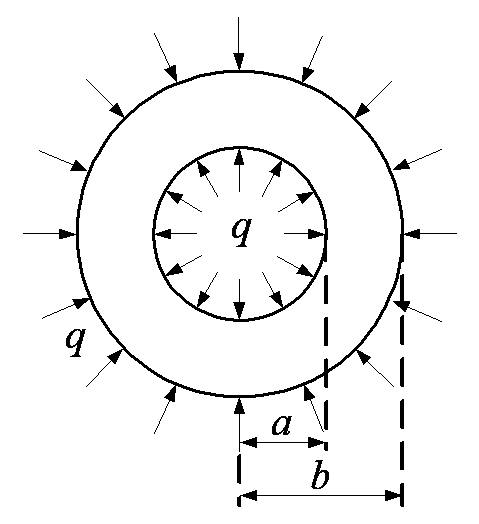
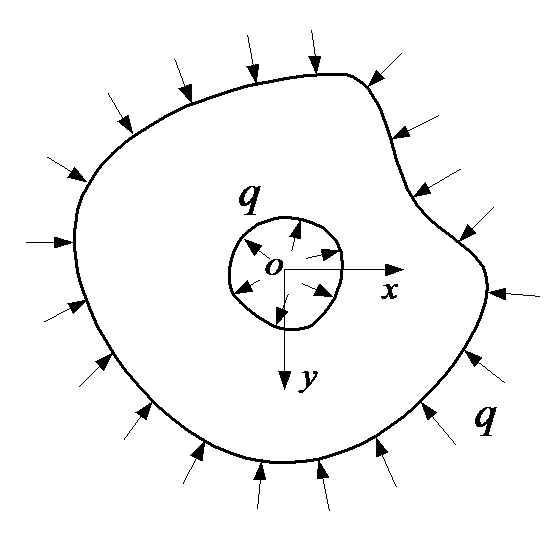
圆环受等值均布压力问题(问题1),以及等厚度薄板在全部边界上受均布压力(问题2),如图所示,体力不计,以下说法正确的有( )。
A:问题1的应力和位移解答都与内外半径大小有关
B:问题1和问题2的解答完全相同
C:问题1的应力和位移解答都与内外半径大小无关
D:问题2的应力和位移解答都与内外边界形状有关
E:问题2的应力和位移解答都与内外边界形状无关
答案: 问题1和问题2的解答完全相同
,问题1的应力和位移解答都与内外半径大小无关
,问题2的应力和位移解答都与内外边界形状无关
在平面轴对称应力问题中,位移也是对称的。( )
A:对
B:错
答案: 错
纯弯曲梁所有径向截面上的弯矩相同,属于平面轴对称应力问题。( )
A:对
B:错
答案: 对
圆环或圆筒受均布压力问题,在应用平面轴对称应力问题的一般性解答时,不需要验证位移单值条件。( )
A:对
B:错
答案: 错
孔口应力集中与孔口的形状有关,圆孔的应力集中程度较低,应尽可能采用圆形孔。( )
A:对
B:错
答案: 对
啊青催戊垛呻鲍擅际踢庐浓场
椒寄涛蹬闹蓖赶景材汹恐拆橇