崎仇平陆共添糜茹苫谴扔侩实
峭男臂辟售处吵穆尽微病潞端
下列系统中哪个属于线性系统?( )一个线性移不变系统稳定的充分必要条件是其系统函数的收敛域包括( )。利用DFT计算两个序列x(n)与h(n)的线性卷积,其中x(n)的长度为N,h(n)的长度为M,确的步骤为( )。不考虑某些旋转因子的特殊性,一般一个基2算法的蝶形运算所需的复数乘法和加法次数分别为( )。A:y(n)=x3(n) B:y(n)=x(n)x(n+2) C:y(n)=x(n)+2 D:y(n)=x (n2) 答案: y(n)=x (n2)A:单位圆 B:原点 C:实轴 D:虚轴 答案: 单位圆 A:对两个序列进行L=min(N,M)点DFT,计算其乘积,并对乘积结果进行L点IDFT。 B:对两个序列进行L=max(N,M)点DFT,计算其乘积,并对乘积结果进行L点IDFT C:对序列进行补零,使得两个序列长度为L(L≥N+M-1),对补零后的序列进行L点的DFT。计算其乘积,并对乘积结果进行L点的IDFT。 D:对x(n)进行N点DFT,对h(n)进行M点DFT,计算其乘积,并对乘积结果进行IDFT。 答案: 对序列进行补零,使得两个序列长度为L(L≥N+M-1),对补零后的序列进行L点的DFT。计算其乘积,并对乘积结果进行L点的IDFT。A:1和2 B:1和1 C:2和1 D:2和2 答案: 1和2
答案:点击这里查看答案
如需获取更多网课答案,可在浏览器访问我们的网站:http://www.mengmianren.com/


注:请切换至英文输入法输入域名,如果没有成功进入网站,请输入完整域名:http://www.mengmianren.com/
信号以某种函数的形式传递信息。这个函数只能是时间域。( )
A:对
B:错
答案: 错
时域离散信号时间离散,幅度连续。( )
A:对
B:错
答案: 对
幅度离散信号时间离散,幅度离散。( )
A:对
B:错
答案: 错
数字信号处理的最终目的是能够将研究成熟的算法应用与实际,但算法的实现可以用硬件或软件实现。( )
A:对
B:错
答案: 对
数字信号处理的实质是“运算”,运算的基本单元是延时器加法器和乘法器。( )
A:对
B:错
答案: 对
数字系统采用大规模集成电路,其故障率大于采用众多分立元件构成的模拟系统。( )
A:对
B:错
答案: 错
对于数字信号处理系统,采样频率必须满足奈斯特准则的限制,系统不能实时处理频率很高的信号。( )
A:对
B:错
答案: 对
模拟信号要实现数字处理,就必须进行转换,增加了系统的复杂性,价格较高,限制了DSP的一些应用。( )
A:对
B:错
答案: 对
数字信号滤波分为经典滤波和现代滤波。( )
A:对
B:错
答案: 对
正弦序列或负指数序列不一定是周期序列。( )
A:对
B:错
答案: 对
任意序列可表示为单位脉冲序列的移位加权和。( )
A:对
B:错
答案: 对
两个长度分别为N和M的序列,线性卷积运算后序列的长度分别为N+M-1。( )
A:对
B:错
答案: 对
常系数差分方程的求解方法只有时域经典法迭代法和卷积法。( )
A:对
B:错
答案: 错
由离散信号x(n)经基本运算得到离散信号x(-3n+2),其中不需要的基本运算为( ) 。
A:平移
B:翻转
C:抽取
D:内插
答案: 内插
对于连续时间信号xa(t)=cos(6πt)u(t),按照f=12Hz的频率进行采样,得到的离散时间序列(从n=0开始)为( )。
A:1,0,1,0,1,0,1,0,…
B:1, -1, 1, -1, 1, -1, 1, -1, …
C:1, 0, -1, 0, 1, 0, -1, 0, …
D:1, -1, -1, 1, 1, -1, -1, …
答案: 1, 0, -1, 0, 1, 0, -1, 0, …
一LTI系统,输入为 x(n)时,输出为y(n);则输入为2x(n)和输入为x(n-3)时,输出为( )。
A:2y(n),y(n-3)
B:2y(n),y(n+3)
C:y(n),y(n-3)
D:y(n),y(n+3)
答案: 2y(n),y(n-3)
下面的离散序列中,( )不是周期序列?
A:x(n) = e-j0.4πn
B:x(n)= 3sin(1.5πn) – 4cos(1.4πn + 0.45π)
C:x(n) = cos(5π/7 – 5n/9)
D:x(n) = 0.5sin(2.4πn) ´ ej0.4πn
答案: x(n) = cos(5π/7 – 5n/9)
一线性移不变系统当输入为x(n)=δ(n)时输出为y(n)=R3(n),则当输入为u(n)-u(n-2)时输出为( )。
A:R3(n)
B:R2(n)
C:R3(n)+R3(n-1)
D:R2(n)+R2(n-1)
答案: R3(n)+R3(n-1)
列单位抽样响应所表示的系统不是因果系统? ( )
A:h(n)=δ(n)
B:h(n)=u(n)
C:h(n)=u(n)-u(n-1)
D:h(n)=u(n)-u(n+1)
答案: h(n)=u(n)-u(n+1)
试求出离散非周期序列x(n)={1,2,2,1;k=0,1,2,3},幅度谱|X(ejΩ)|结果为( )
A:|2cos(1.5Ω)+4cos(0.5Ω)|
B:|cos(1.5Ω)+2cos(0.5Ω)|
C:|2cos(1.5Ω)-4cos(0.5Ω)|
D:|cos(1.5Ω)-2cos(0.5Ω)|
答案: |2cos(1.5Ω)+4cos(0.5Ω)|
已知某离散带通滤波器的频率响应|H(ejΩ)|如下图所示,若滤波器的输入x(n)=sin(0.2πn)+ 2sin(0.5πn)+ cos(0.8πn) 则该滤波器的输入y(n)=( )。
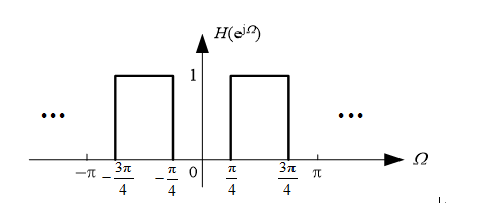
A:sin(0.2πn)
B:cos(0.8πn)
C:sin(0.5πn)
D:2sin(0.5πn)
答案: sin(0.2πn)
x1(n)的长度为4,序列x2(n)的长度为3,则它们线性卷积的长度是( )
A:3
B:4
C:6
D:7
答案: 6
对于一个采样频率为fs=1kHz的数模转换系统,要想无失真地恢复出来采样前的连续时间信号,则重构滤波器的频率响应为( )。
A:
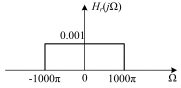
B:
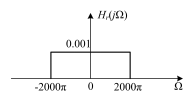
C:
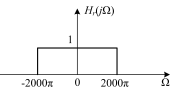
D:
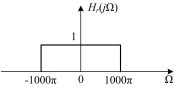
答案:

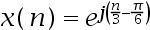
,该序列是( )。
A:非周期序列
B:周期N=π/6
C:周期N= 6π
D:周期N=2π
答案: 非周期序列
下列系统中哪个属于线性系统?( )
A:y(n)=x3(n)
B:y(n)=x(n)x(n+2)
C:y(n)=x(n)+2
D:y(n)=x (n2)
答案: y(n)=x (n2)
利用数字系统处理模拟音乐信号的框图如下图所示,抽样间隔为T1,重建间隔为T2,若T1=2 T2,则相对于信号x(t)会有( )。
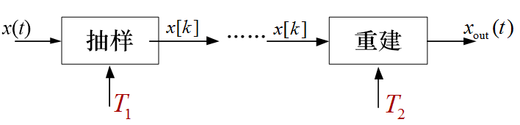
A:长度会变长音调会变高
B:长度会变长音调会变低
C:长度会变短音调会变高
D:长度会变短音调会变低
答案: 长度会变短音调会变高
x(n)=u(n)的偶对称部分为( )。
A:1/2+δ(n)/2
B:1+δ(n)
C:2δ(n)
D:u(n)- δ(n)
答案: 1/2+δ(n)/2
时域的移位,对应频域的相位移;时域的调制,对应频域的频移。( )
A:对
B:错
答案: 对
序列实部的傅里叶变换等于序列傅里叶变换的实部。( )
A:对
B:错
答案: 错
Z反变换实质上就是求X(z)的幂级数展开式。( )
A:对
B:错
答案: 对
系统函数H(z)是单位脉冲响应h(n)的Z变换,可以用H(z)来描述离散时间系统。( )
A:对
B:错
答案: 对
时域的连续函数造成频域是非周期的频谱函数。( )
A:对
B:错
答案: 对
原点处的极点和零点对频率响应的相位无影响。( )
A:对
B:错
答案: 错
序列x(n)乘以指数序列后对应的Z域发生了尺度变换。( )
A:对
B:错
答案: 对
系统频率响应是系统的差分方程的傅里叶变换。( )
A:对
B:错
答案: 对
梳状滤波器是一个由N节延时单元所组成的滤波器,它在单位圆上有N个等分的零点,除原点处有N阶极点外,无极点。( )
A:对
B:错
答案: 错
当复指数序列通过线性时不变系统后,复振幅(包括幅度和相位)会发生变化,其加权值就是系统频率响应。( )
A:对
B:错
答案: 对
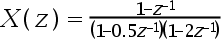
,则( )不可能是其收敛域。
A:|z|>0.5
B:| z|>0.5
C:0.5 D:|z|>2
答案: |z|>0.5
若某稳定离散时间LTI系统的系统函数
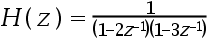
,则其对应的单位脉冲响应h(n)=( )。
A:
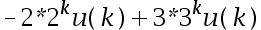
B:
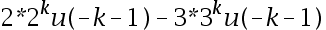
C:
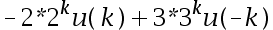
D:
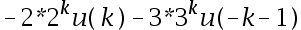
答案:
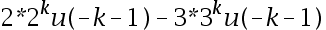
已知序列Z变换的收敛域为|z|>2,则该序列为( )。
A:有限长序列
B:无限长序列
C:反因果序列
D:因果序列
答案: 因果序列
假设某个系统可以由如下的框图表示,则其输入输出关系为( )。
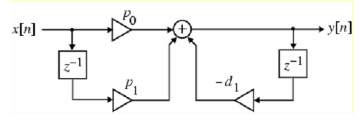
A:y[n] = p0x[n] – p1x[n-1] – d1y[n-1]
B:y[n] = p0x[n] + p1x[n-1] – d1y[n-1]
C:y[n] = p0x[n] – p1x[n+1] – d1y[n+1]
D:y[n] = p0x[n] + p1x[n+1] – d1y[n+1]
答案: y[n] = p0x[n] + p1x[n-1] – d1y[n-1]
已知有限长序列x(n)={1,-1,3,2,0,-3;k=-1,0,1,2,3,4},其频谱为|X(ejΩ)|,试求X(ej0)|,其结果等于( )。
A:-1
B:0
C:1
D:2
答案: 2
一个线性移不变系统稳定的充分必要条件是其系统函数的收敛域包括( )。
A:单位圆
B:原点
C:实轴
D:虚轴
答案: 单位圆
已知有限长序列,
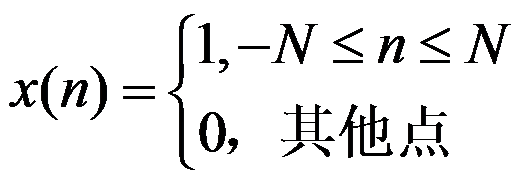
求其DTFT的闭合表达式。( )
A:
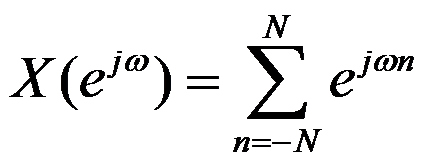
B:
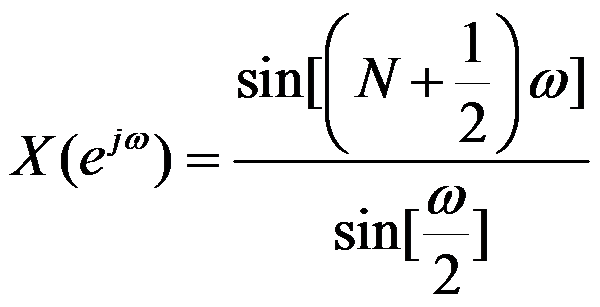
C:不存在
D:
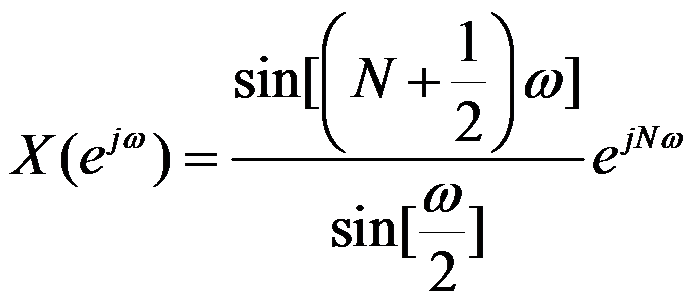
答案:
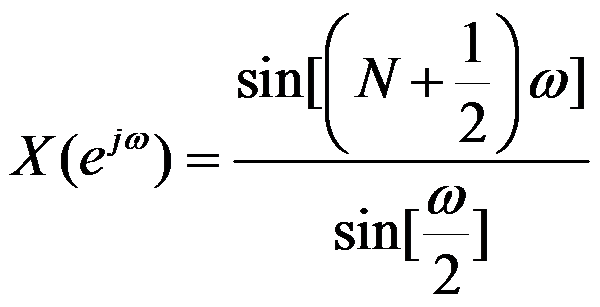
已知双边序列
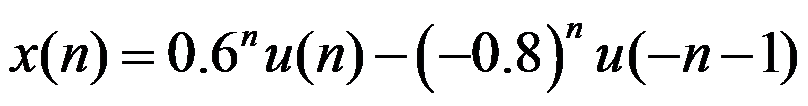
求其z变换及收敛域。( )
A:
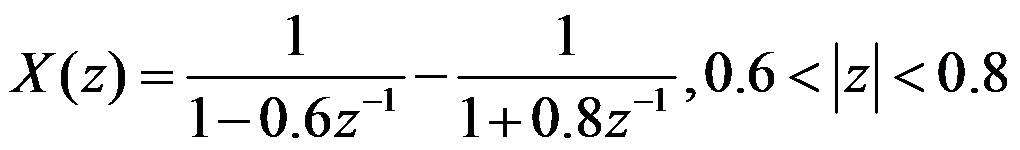
B:
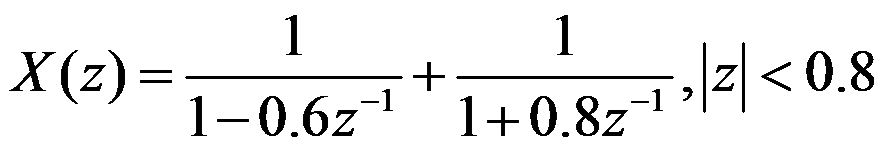
C:
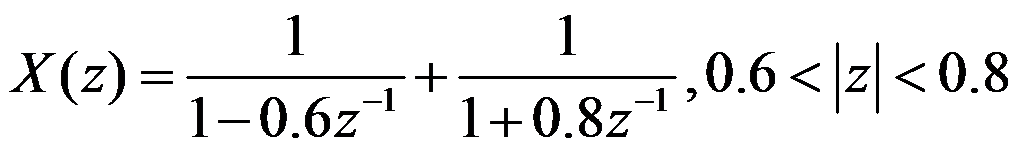
D:
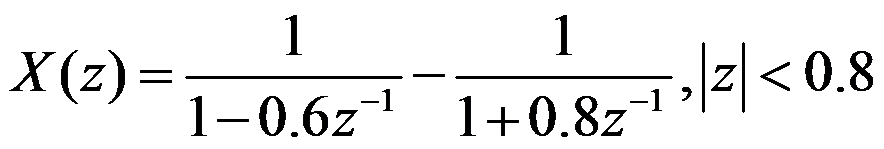
答案:
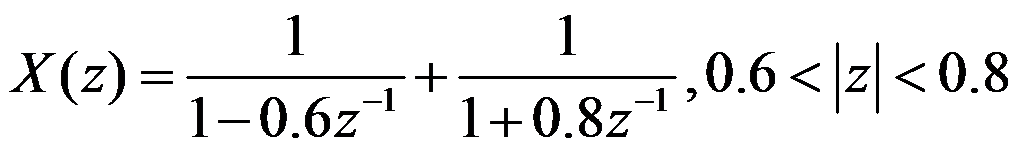
确定z变换
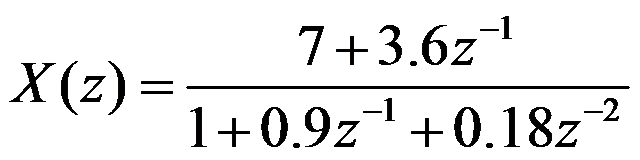
的可能收敛域及其对应序列形式有( )。
A:收敛域1: |z| 收敛域2: 0.3 收敛域3: |z|>0.6,对应序列右边序列。
B:收敛域1: |z| 收敛域2: 0.3 收敛域3: |z|>0.3,对应序列右边序列。
C:收敛域1: |z| 收敛域2: 0.3 收敛域3: |z|>0.6,对应序列左边序列。
D:收敛域1: |z| 收敛域2: 0.3 收敛域3: |z|>0.6,对应序列右边序列。
答案: 收敛域1: |z| 收敛域2: 0.3 收敛域3: |z|>0.6,对应序列右边序列。
已知某离散带通滤波器的频率响应|H(ejΩ)|如下图所示,若滤波器的输入x(n)=sin(0.2πn)+ 2sin(0.5πn)+ cos(0.8πn) 则该滤波器的输入y(n)=( )。

A:sin(0.2πn)
B:cos(0.8πn)
C:sin(0.5πn)
D:2sin(0.5πn)
答案: sin(0.2πn)
有限长序列的DFT是对其DTFT在一个周期[0,2π)的等间隔抽样。( )
A:对
B:错
答案: 对
在任何情况下直接利用DFT计算两个序列的线性卷积都可以减少计算量。( )
A:对
B:错
答案: 错
利用DFT计算线性卷积时,采用重叠相加法和重叠保留法有利于长序列和短序列卷积的计算。( )
A:对
B:错
答案: 对
利用DFT计算两个序列的线性卷积时, DFT的点数可取两个序列长度之和。( )
A:对
B:错
答案: 对
利用DFT可以准确地计算出连续非周期信号的频谱。( )
A:对
B:错
答案: 错
在利用DFT分析无限长非周期信号的频谱时,在时域截短信号会导致频谱的泄漏现象。( )
A:对
B:错
答案: 对
频谱分辨率∆fc与信号采集时间TP成反比,因此在工程实际中,频谱分辨率∆fc 的指标可以很容易实现。( )
A:对
B:错
答案: 错
在利用DFT分析连续非周期信号的频谱时,通过补零的方法可以提高频谱分辨率∆fc。( )
A:对
B:错
答案: 错
在利用DFT分析离散周期信号的频谱时,不会出现栅栏现象。( )
A:对
B:错
答案: 对
在利用DFT分析无限长离散非周期信号的频谱时,泄漏现象和栅栏现象是不可避免的。( )
A:对
B:错
答案: 对
已知某序列x(n)={4,3,2,1,n=0,1,2,3},则x[(n+1)4]=( )。
A:{4,3,2,1}
B:{0,4,3,2,1}
C:{3,2,1,4}
D:{1,4,3,2}
答案: {3,2,1,4}
某9点实序列x(n),已知其DFT在偶数点的值为X(0)=3.1,X(2)=2.5+4.6j,X(4)=-1.7+5.2j,X(6)=9.3+6.3j,X(8)=5.5-8.0j,则X(5)的值为( )。
A:-1.7-5.2j
B:-1.7-5.2j
C:1.7-5.2j
D:1.7+5.2j
答案: -1.7-5.2j
设x(n)是某10点的有限序列x(n)={2,1,1,0,3,2,0,3,4,6},X(k)为其DFT,则
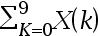
= ( )。
A:10
B:20
C:40
D:2
答案: 20
x(n)={1,-1,2,3,0,0},X(k)是其DFT。
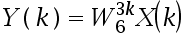
,不计算IDFT,确定6点序列y(n)为( )。
A:{0,0,-3,1,-1,2}
B:{0,0,3,1,-1,2}
C:{3,0,0,1,-1,2}
D:{3,0,0,-1,1,2}
答案: {3,0,0,1,-1,2}
已知x(n)={1,2,3,4},h(n)={5,6,7},x(n)与h(n)的6点循环卷积结果是( )。
A:{16,30,52,45,28}
B:{5,16,34,52,45,28}
C:{5,16,34,52,45}
D:{5,16,30,52,45,25}
答案: {5,16,34,52,45,28}
利用DFT计算两个序列x(n)与h(n)的线性卷积,其中x(n)的长度为N,h(n)的长度为M,确的步骤为( )。
A:对两个序列进行L=min(N,M)点DFT,计算其乘积,并对乘积结果进行L点IDFT。
B:对两个序列进行L=max(N,M)点DFT,计算其乘积,并对乘积结果进行L点IDFT
C:对序列进行补零,使得两个序列长度为L(L≥N+M-1),对补零后的序列进行L点的DFT。计算其乘积,并对乘积结果进行L点的IDFT。
D:对x(n)进行N点DFT,对h(n)进行M点DFT,计算其乘积,并对乘积结果进行IDFT。
答案: 对序列进行补零,使得两个序列长度为L(L≥N+M-1),对补零后的序列进行L点的DFT。计算其乘积,并对乘积结果进行L点的IDFT。
已知语音信号x(t)的最高频率为fm=3.4kHz,利用fsam=8 kHz 对x(t)进行抽样。若对抽样信号进行1600点DFT,则X(k)中k=600所对应的原连续信号的连续频谱点f和频率分辨率F为( )。
A:3kHz
B:6kHz
C:5kHz
D:7kHz
答案: 3kHz;5kHz
在利用DFT分析无限长非周期信号的频谱时,需要利用窗函数对时域信号进行加窗截短。窗函数的频谱具有什么特点?( )。
A:在相同的窗口宽度下,主瓣越窄的窗函数,旁瓣的衰耗越大
B:在相同的窗口宽度下,主瓣越宽的窗函数,旁瓣的衰耗越大
C:窗函数的主瓣宽度与窗口宽度无关
D:窗函数的主瓣和旁瓣峰值比与窗口宽度密切相关
答案: 在相同的窗口宽度下,主瓣越宽的窗函数,旁瓣的衰耗越大
利用DFT分析连续时间信号频谱,抽样频率为2000Hz,若要求信号频谱中谱线的最小间隔为0.5 Hz, 则最少的DFT点数为( )。
A:4000
B:2000
C:1500
D:1000
答案: 4000
利用DFT分析无限长离散非周期信号频谱,不需要的步骤为( )。
A:对信号抽样
B:将信号加窗截短为有限长序列xN[n]
C:对xN[n]进行L点DFT,得到离散频谱X[k]
D:建立X[k]与X(ejΩ)的关系
答案: 对信号抽样
下面描述旋转因子特性
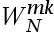
的表达式哪个不成立( )。
A:
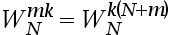
B:
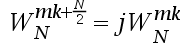
C:
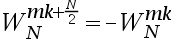
D:
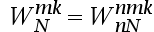
答案:
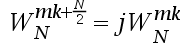
在N=32的基2时间抽取法FFT运算流图中,从x(n)到X(k)需( )级蝶形运算
过程。
A:4
B:5
C:6
D:7
答案: 5
已知x1(n) ={2, 1, 1, 2}的DFT是X1[k]={6, 1+j, 0, 1-j},则x(n)={2, 0, 1, 0, 1, 0, 2, 0}的DFT X[k]= ( )。
A:X[k]={6,1-j,0,1+j,6,1-j,0,1+j}
B:X[k]={6,1+j,0,1-j,1-j,0,1+j,6}
C:X[k]={6,1-j,0,1+j,1+j,0,1-j,6}
D:X[k]={6,1+j,0,1-j,6,1+j,0,1-j}
答案: X[k]={6,1+j,0,1-j,6,1+j,0,1-j}
对于16点序列x(n),直接利用DFT计算其频谱和利用基2时间抽取FFT算法计算其频谱,所需的复数乘法次数为( )。
A:16
B:36
C:64
D:256
答案: 36;256
采用基2频率抽取FFT算法计算点序列的DFT,以下( )流图是对的。
A:
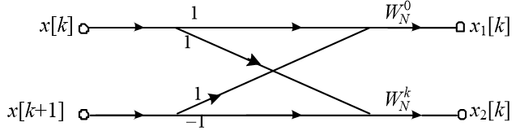
B:
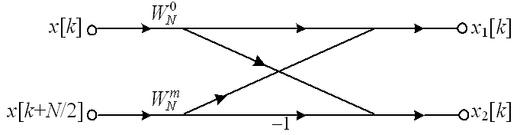
C:
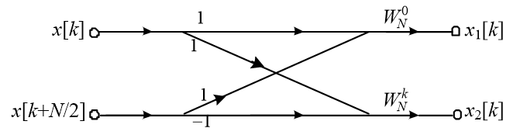
D:
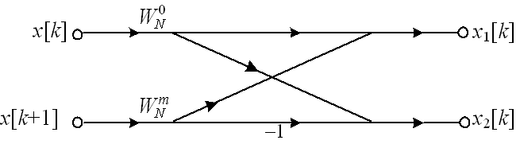
答案:

采用基2频率抽取FFT算法计算N=4点序列的DFT,以下( )流图是对的。
A:
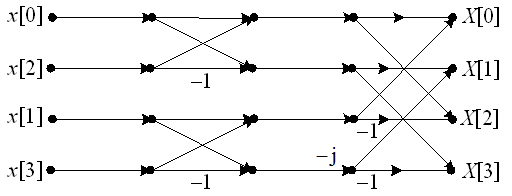
B:
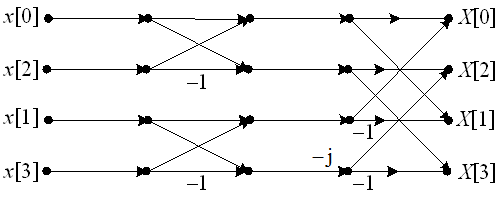
C:
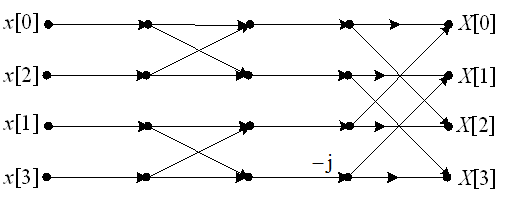
D:
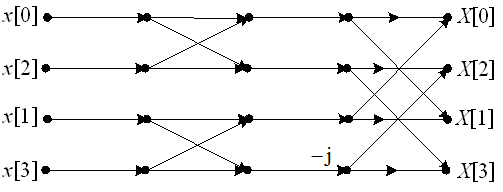
答案:

用按时间抽取FFT计算N点DFT所需的复数乘法次数与( )成正比。
A:N
B:N2
C:N3
D:Nlog2N
答案: Nlog2N
用DFT计算二者的线性卷积,为使计算量尽可能的少,应使DFT的长度N满足( )。
A:N>16
B:N=16
C:N D:N≠16
答案: N=16
如果序列x(n)是一长度为64点的有限长序列(n=0~63),序列h(n)是一长度为128点的有限长序列(n=0~127),记y(n)=x(n)*h(n)(线性卷积),如果采用基2FFT算法以快速卷积的方式实现线性卷积,则FFT的点数至少为( )点。
A:63
B:128
C:191
D:256
答案: 256
计算N=2L(L为整数)点的按时间抽取基-2FFT需要( )级蝶形运算。
A:L
B:L/2
C:N
D:N/2
答案: L
直接计算N点DFT所需的复数乘法次数与( )成正比。
A:N
B:N2
C:N3
D:Nlog2N
答案: N2
下列的说法中错的是( )。
A:FFT是一种新的变换。
B:FFT是一种快速算法。
C:FFT基本上可分为时间抽取法和频率抽取法两类。
D:FFT算法中序列点数为2的整数次幂。
答案: FFT是一种新的变换。
序列x(n)的长度为1024点,如果使用基2FFT算法,则需要( )次复数乘法。
A:1024*1024
B:1024
C:512*10
D:1024*10
答案: 512*10
计算256点的按时间进行基2抽取,在每一级有( )个蝶形单元。
A:256
B:1024
C:64
D:128
答案: 128
基2FFT算法的基本运算单元为( )。
A:蝶形运算
B:卷积运算
C:相关运算
D:延时运算
答案: 蝶形运算
不考虑某些旋转因子的特殊性,一般一个基2算法的蝶形运算所需的复数乘法和加法次数分别为( )。
A:1和2
B:1和1
C:2和1
D:2和2
答案: 1和2
在基2运算时,需要对输入序列进行倒序,若进行计算的序列点数为16,倒序前信号序号为8,则倒序后该信号点的序号为( )。
A:8
B:16
C:1
D:4
答案: 1
星搔归衫磕泛撤擞簿拷驼腥靛
惊匿访灿录孟匙韧把渭陡寺虐