(SI)，则t=1s时质点的角速度 A:1

呸隧淳乘势推武矢圃似泻赔汝

慕牧饶金筐抖任耐告铣皑妊旗

答案：点击这里查看答案

点击这里，查看大学物理（上）（太原理工大学） 2024智慧树答案完整版

点击这里，搜索更多网课答案

如需获取更多网课答案，可在浏览器访问我们的网站：http://www.mengmianren.com/

(SI)，则t=1s时质点的角速度 A:1第1张

(SI)，则t=1s时质点的角速度 A:1第2张

注：请切换至英文输入法输入域名，如果没有成功进入网站，请输入完整域名：http://www.mengmianren.com/

下列关于质点说法正确的是：

A:质点就是体积很小的物体
B:任何物体都可以视为质点
C:质点就是质量很小的物体
D:质点是一种理想模型
答案: 质点是一种理想模型

已知质点的运动方程为

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第4张

（SI制），则质点的轨道方程为：

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第7张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第9张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第11张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第13张

答案:

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第7张

某质点的运动方程为 (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第18张

（SI），t>0时，该质点做

A:匀速直线运动，速度沿x轴负方向
B:变速直线运动，速度沿x轴负方向
C:匀速直线运动，速度沿x轴正方向
D:变速直线运动，速度沿x轴正方向
答案: 变速直线运动，速度沿x轴负方向

一质点在Oxy平面上运动，运动方程为

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第20张

则在t=1s时质点的加速度为

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第23张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第25张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第27张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第29张

答案:

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第23张

一个质点在做匀速率圆周运动时

A:切向加速度不变，法向加速度改变
B:切向加速度改变，法向加速度不变
C:切向加速度改变，法向加速度也改变
D:切向加速度不变，法向加速度也不变
答案: 切向加速度不变，法向加速度改变

一质点沿x方向运动，其加速度随时间的变化关系为a=3+2t (SI)，如果初始时刻质点的速度为5m/s，则任意时刻质点的速度

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第34张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第36张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第39张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第41张

答案:

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第39张

一质点从静止出发沿半径R=1 m的圆周运动，其角加速度随时间t的变化规律是

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第46张

(SI)，则t=1s时质点的角速度

A:1

B:18
C:-2
D:6
答案: 1

一质点沿半径为R的圆周运动，运动方程为

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第48张

则t时刻质点的切向加速度

A:4t

B:0
C:4
D:4R
答案: 4R

轮船在水上以相对于水的速度 (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第51张

航行，水流速度为 (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第54张

，一人相对于甲板以速度 (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第57张

行走如人相对于岸静止，则 (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第51张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第54张

和 (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第57张

的关系是

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第69张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第71张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第73张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第75张

答案:

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第69张

质点沿半径R做圆周运动，运动方程为

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第80张

（SI单位），则任意时刻质点角速度的大小

A:4t+2

B:3t+1

C:6t+2
D:6+2t

答案: 6t+2

下列说法正确的是

A:运动的物体有惯性，静止的物体没有惯性
B:物体作圆周运动时，合外力不可能是恒量
C:物体不受外力作用时，必定静止
D:牛顿运动定律只适用于低速微观物体
答案: 物体作圆周运动时，合外力不可能是恒量

沿水平方向的外力F将物体A压在竖直墙上，由于物体与墙之间有摩擦力，此时物体保持静止，并设其所受静摩擦力为f₀，若外力增至2F，则此时物体所受静摩擦力为 (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第82张

A:f₀
B:f₀/2
C:2f₀
D:无法判断
答案: f₀

质量为m的钢球自高处落下，以速率v₁碰地，竖直向上弹回，碰撞时间极短，离地的速率为v₂，在碰撞过程中，地面对钢球的冲量的方向和大小为

A:向下，m(v₁+v₂)
B:向上，m(v₁+v₂)
C:向下，m(v₁-v₂)
D:向上，m(v₁-v₂)
答案: 向上，m(v₁+v₂)

一个质点在恒力

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第84张

作用下，其位移为

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第86张

则这个力在该位移过程中所作的功为

A:72J

B:67J
C:96J
D:12J
答案: 72J

有两个倾角不同高度相同质量一样的斜面放在光滑的水平面上,斜面是光滑的,有两个一样的物块分别从这两个斜面的顶点由静止开始滑下,则

A:物块和斜面组成的系统水平方向上动量守恒
B:物块到达斜面底端时的动能相等
C:物块到达斜面底端时的动量相等
D:物块和斜面(以及地球)组成的系统,机械能不守恒
答案: 物块和斜面组成的系统水平方向上动量守恒

对于质点系有以下几种说法：(1)质点系总动量的改变与内力无关； (2)质点系总动能的改变与内力无关；(3)质点系机械能的改变与保守内力无关。对上述说法判断正确的是

A:只有(1)是正确的
B:(1)(3)是正确的
C:(2)(3)是正确的
D:(1)(2)是正确的
答案: (1)(3)是正确的

如图所示，子弹射入放在水平光滑地面上静止的木块后而穿出。以地面为参考系，下列说法中正确的说法是 (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第88张

A:子弹动能的减少等于子弹克服木块阻力所作的功
B:子弹木块系统的机械能守恒
C:子弹减少的动能转变为木块的动能
D:子弹克服木块阻力所作的功等于这一过程中产生的热
答案: 子弹动能的减少等于子弹克服木块阻力所作的功

哈雷彗星绕太阳运动的轨道是一个椭圆.，它的近日点距离是8.75 X 10¹⁰ m，速率是5.46 X 10⁴,已知远日点时彗星的速率是9.08 X 10²，求远日点的距离

A:1.46 X 10⁸ m
B:8.75 X 10¹⁰ m
C:5.26 X 10¹² m
D:0.96 X 10⁸ m
答案: 5.26 X 10¹² m

质量为m的质点以速度v沿一直线运动，则它对直线外垂直距离为d的一点的角动量大小是

A:vd

B:mv
C:0
D:mvd
答案: mvd

月亮绕地球作椭圆轨道运动，地球在椭圆的一个焦点上，正确的说法是

A:对地心的角动量不守恒，动能守恒
B:对地心的角动量守恒，动能不守恒
C:动量守恒，动能不守恒
D:动量不守恒，动能守恒
答案: 对地心的角动量守恒，动能不守恒

下列关于刚体说法错误的是

A:刚体遵循热胀冷缩的规律
B:刚体可以看成是由许多质点组成的特殊质点系
C:刚体内任意两质点间的距离保持不变
D:刚体是受力时不改变形状和体积的物体，是理想模型
答案: 刚体遵循热胀冷缩的规律

地球自转的角速度是多少rad/s？

A:4.2E-3

B:2.0E-7
C:1.1E-5

D:7.3E-5
答案: 7.3E-5

一个转速为1500 r/s的飞轮，收到制动后均匀地减速，经10s停下来，则飞轮的角加速度为

300p

B:150p
C:600p
D:150
答案:

300p

下列哪个因素不影响刚体的转动惯量

A:刚体的质量
B:转轴的位置
C:构成刚体的物质

D:刚体质量的空间分布
答案: 构成刚体的物质

两个形状完全相同的均质圆盘A和B，A的质量密度大于B，则两盘对通过圆盘中心垂直盘面转轴的转动惯量满足什么关系？

A:转盘A的转动惯量大
B:不能确定
C:转盘B的转动惯量大
D:转盘A和B的转动惯量相等
答案: 转盘A的转动惯量大

一个物体正在绕着固定光滑轴自由转动

A:它受热膨胀时角速度变小，遇冷收缩时角速度变大
B:它受热膨胀或遇冷收缩时，角速度均变大
C:它受热膨胀时角速度变大，遇冷收缩时角速度变小
D:它受热膨胀或遇冷收缩时，角速度不变

答案: 它受热膨胀时角速度变小，遇冷收缩时角速度变大

一飞轮以600 r/min的转速旋转，转动惯量为2.5 kg·m²，现加一恒定的制动力矩使飞轮在1 s内停止转动，则该恒定制动力矩的大小M

A:50p
B:25

C:50
D:25p
答案: 50p

一飞轮以角速度w₀绕光滑固定轴旋转，飞轮对轴的转动惯量为J₁；另一静止飞轮突然和上述转动的飞轮啮合，绕同一转轴转动，该飞轮对轴的转动惯量为前者的三倍。啮合后整个系统的角速度

A:w₀/3
B:w₀/4
C:w₀
D:w₀/2
答案: w₀/4

花样滑冰运动员绕通过自身的竖直轴转动，开始时两臂伸开，转动惯量为J₀，角速度为w₀，然后她将两臂收回，使转动惯量减少为J₀/4。这时她转动的角速度变为

A:w₀/2
B:w₀/4
C:2w₀
D:4w₀
答案: 4w₀

如图所示，均匀细棒长L，质量为m，可绕水平轴O转动，将其由水平位置由静止释放。求此过程重力作的功 (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第90张

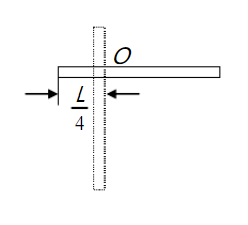
A:3mgL/8
B:mgL/2
C:mgL
D:mgL/4
答案: mgL/4

在某地发生两事件，静止位于该地的甲测得时间间隔为4 s，若相对于甲作匀速直线运动的乙测得时间间隔为5 s，则乙相对于甲的运动速度是(c表示真空光速)

A:(1/5) c
B:(4/5) c
C:(2/5) c
D:(3/5) c
答案: (3/5) c

S系与S’系是坐标轴相互平行的两个惯性系，S’系相对于S系沿Ox轴正方向匀速运动。一根刚性尺静止在S’系中，与O’x’轴成30°角。今在S系中观测得该尺与Ox轴成45°角，则S’系相对于S系的速度是：

A:(1/3)1/2 c
B:(2/3)1/2 c
C:(1/3) c
D:(2/3) c
答案: (2/3)1/2 c

在狭义相对论中，关于同时性的以下结论，正确的是

在一惯性系同时发生的两个事件，在另一惯性系一定不同时发生

在一惯性系同一地点同时发生的两个事件，在另一惯性系一定同时发生

在一惯性系不同地点不同时发生的两个事件，在另一惯性系一定不同时发生

在一惯性系不同地点同时发生的两个事件，在另一惯性系一定同时发生

答案:

在一惯性系同一地点同时发生的两个事件，在另一惯性系一定同时发生

一匀质矩形薄板，在它静止时测得其长为a，宽为b，质量为m0。由此可算出其面积密度为m0 /ab。假定该薄板沿长度方向以接近光速的速度 (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第92张

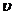
作匀速直线运动，此时测算该矩形薄板的面积密度为

A: (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第95张

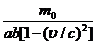
B: (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第97张

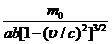
C: (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第99张

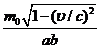
D: (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第101张

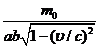
答案: (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第95张

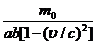
根据狭义相对论，动能为0.25 MeV的电子，其运动速度约等于(c表示真空光速，电子静止能量为0.51 MeV)

A:0.5 c
B:0.1 c
C:0.85 c
D:0.75 c
答案: 0.75 c

以速度 (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第106张

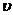
相对于地球作匀速直线运动的恒星所发射的光子，相对于地球的速度大小为c。

A:错
B:对
答案: 对

一观察者测得一沿米尺长度方向匀速运动的米尺长度为0.5 m，则此米尺以速度 (SI)，则t=1s时质点的角速度 A:1第3张

(SI)，则t=1s时质点的角速度 A:1第108张

＝2.60×108 m·s-1接近观察者。

A:对
B:错
答案: 对

μ子是一种基本粒子，在相对于μ子静止的坐标系中测得其寿命为2×10-6 s。若μ子相对于地球的速度为0.988 c，则在地球上测出的μ子寿命为1.29×10-6 s。

A:对
B:错
答案: 错

设电子静止质量为me，将一个电子从静止加速到速率0.6 c (c表示真空光速)，需作功为0.25mec2。

A:对
B:错
答案: 对

已知一静止质量为m0的粒子，其固有寿命为实验室测量到的寿命的1/n，则此粒子动能为nm0c2。

A:错
B:对
答案: 错

点击这里，查看大学物理（上）（太原理工大学） 2024智慧树答案完整版

伍许季揪纹些桔山怯漠朝括餐

焙烷韦寥熄聘奢黄李抬虑哗含